Analysis and Synthesis of Logic Functions using Decoders 
Introduction
About the Experiment
This experiment enables a student to learn
- How to realize functionality of a 3-to-8 line active low Decoder viz. 74138 IC. That is on setting the two active low and one active high enable inputs to proper level, one can verify that one and only one of the eight active low outputs is asserted based on the values assigned to three select input.
- How to cascade two 74138 IC's to implement a 4-to-6 active low decoder.
Theory
Part1
IC 74138 works as a 3-to-8 active low decoder,based on the values assigned to three select inputs of the three enable inputs, G1 must be made high value while G2A and G2B must be low. The eight active low inputs (Y0 to Y7) correspond to eight maxterms (M0 to M7) or in other words, component of the corresponding minterms m0-m7. For example, Y0 = component of C B A = C+B+A.
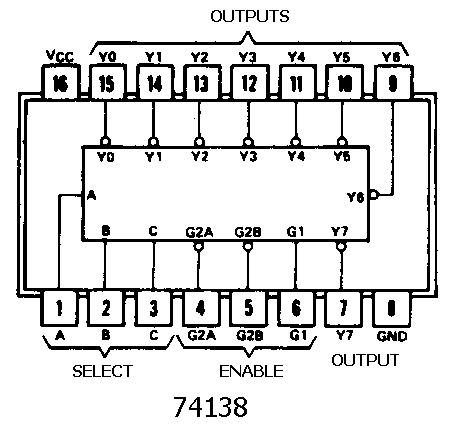
Figure 1 (IC 74138)
| $$ \overline { G2A } $$ | $$ \overline { G2B } $$ | G1 | C | B | A | $$ \overline{ Y0 } $$ | $$ \overline{ Y1 } $$ | $$ \overline{ Y2 } $$ | $$ \overline{ Y3 } $$ | $$ \overline{ Y4 } $$ | $$ \overline{ Y5 } $$ | $$ \overline{ Y6 } $$ | $$ \overline{ Y7 }$$ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | L | H | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| L | L | H | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| L | L | H | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| L | L | H | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| L | L | H | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| L | L | H | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| L | L | H | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| L | L | H | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Figure 2 Truth table for 3 to 8 decoder
Part2
Cascading two 74138 IC(Two 3 to 8 active low decoder) we can achieve a 4 to 16 active low decoder.
G2A and G2B inputs of the first IC(74138) and G1 input of 2nd IC(74138) are shorted and it acts as MSB of 4 binary select input . G2A &G2B of second IC(74138) is kept low.G1 of 1st IC is kept always high.
Figure 3: 4 to 16 decoder cascadeding two 3 to 8 decoder
| Select Inputs | 1st Decoder | 2nd Decoder | |||||||||||||||||
| D | C | B | A | Y0 | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y0 | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Figure 4 : Truth table for 4 to 16 decoder
Part 3
A decoder with active high outputs generates minterms. Whereas, a decoder with active low outputs generates maxterms (i.e. complements of the corresponding minterm). Thus, if a function is specified as a sum of minterms or equivalently as a product of maxterms, it can be realized by a decoder with active low outputs and additional AND/NAND gates.
For example, consider the following
F1 (A,B,C) = Σ m (1,2)
F2 (A,B,C) = Σ m (0,1,2,3,4,5)
